Capítulos de ese calibre ha habido y habrá. Este capítulo resulta más llamativo de lo normal debido a que rompe los esquemas habituales. Me ha encantado. Pero espero que semejantes rarezas no se repitan. Primero: porque le arrebatarían la magia a este episodio tan especial, y segundo: porque si lo especial se repite demasiado, la seria cambiaría lo que es... MLP está bien como está, y este episodio me ha parecido fantástico. Aunque no le pondría un 10 por ese HYPE super gordo que tiene. El exceso de hype suele llevar a extremos, tanto negativos, como positivos (en las opiniones).
Esto no lo digo por nadie en especial, si no en general, así que espero que no se me malinterprete. De mi opinión al respecto de la de referee ya he hablado tranquilamte con él. Y la respeto al 100% aunque no la comparta. Lo digo por si alguien comenta o piensa que me refiero concretamente a él o algo... No es el caso. Que quede bien clarito.
Si fuera de otra forma, no dudaría en dejarlo claro también.
[05x09] Slice of Life
Re: [05x09] Slice of Life
La vida es tan bonita como tú quieres que sea, pero sólo es una. Por eso no te canses de ella. Da igual que no hagas o digas nada que parezca "importante" pues tu mera existencia ya es importante para alguien.




-

Ignatius - Stallion/Mare

- Mensajes: 654
- Registrado: 04 Abr 2015, 22:53
- Ubicación: En tierras de tréboles y birra
- Sexo: Masculino
- Pony preferido: Pinkie/CMC/Luna/SG/T
Re: [05x09] Slice of Life
Por cierto..... ¿que hacia allí una cría de changeling?
Mi pony test de perosnalidad.........Just as Pinkie planned
Spoiler:
-

amadeus_dark - Stallion/Mare

- Mensajes: 828
- Registrado: 29 Abr 2013, 12:32
- Sexo: Masculino
- Pony preferido: Rainbow Dash
Re: [05x09] Slice of Life
Foxer, voy a citar parte de tu mensaje para que veas la contradicción que contiene.
Y ese es el problema. Es canon. Es maldito canon y el canon es rey. Y cuando alguien te venga con el cuento de Bon Bon Agente Secreto, ve tú y dile que no es canon. Porque lo es.
Puedes decir que los comics son canon o no, puedes decir que Equestria Girls es canon o no. Pero esto? Este es el maldito episodio 9 de la quinta temporada. Y como tal, es canon.
Esto mismo, hecho por un fan, me hubiera parecido genial. Esto mismo, hecho fuera de la serie estándar como tal, me hubiera parecido genial. Pero todas esas cosas absurdas, ahora son canon. Porque este es un episodio regular, por muy número 100 que sea, de My Little Pony: Friendship is Magic, y como tal lo he valorado.
Os recuerdo a todos que hay gente que evita los spoilers de todo tipo, también. Si un episodio es terrible como episodio 83, por decir algo, también es terrible como episodio 100. Quieres hacer un especial? Hazlo, pero como extra. Así podrás afirmar que no has roto el canon. No se ha hecho así, y así lo he valorado.
Un usuario de este foro me ha pedido que explicara los motivos de mi nota, y lo he hecho. No me hagáis decir que pienso de la reacción que ha habido después.
PS: Gracias, Ignatius, por tu forma de llevar el tema. Así debería ser siempre.
foxer7 escribió en 14 Jun 2015, 03:21:me refiero a k de fan service y cosas "no canon" iba la cosa. de verdad te crees k van a sacar lo de bom bom o lo de gumy otra vez??
como dice, este capitulo podria considerarse aparte, pero creo k cumple esplendidamente su funcion de soltar locuras y pasarte el capitulo diciendo "o dios!" "wtf!" "es canon!".
Y ese es el problema. Es canon. Es maldito canon y el canon es rey. Y cuando alguien te venga con el cuento de Bon Bon Agente Secreto, ve tú y dile que no es canon. Porque lo es.
Puedes decir que los comics son canon o no, puedes decir que Equestria Girls es canon o no. Pero esto? Este es el maldito episodio 9 de la quinta temporada. Y como tal, es canon.
Esto mismo, hecho por un fan, me hubiera parecido genial. Esto mismo, hecho fuera de la serie estándar como tal, me hubiera parecido genial. Pero todas esas cosas absurdas, ahora son canon. Porque este es un episodio regular, por muy número 100 que sea, de My Little Pony: Friendship is Magic, y como tal lo he valorado.
Os recuerdo a todos que hay gente que evita los spoilers de todo tipo, también. Si un episodio es terrible como episodio 83, por decir algo, también es terrible como episodio 100. Quieres hacer un especial? Hazlo, pero como extra. Así podrás afirmar que no has roto el canon. No se ha hecho así, y así lo he valorado.
Un usuario de este foro me ha pedido que explicara los motivos de mi nota, y lo he hecho. No me hagáis decir que pienso de la reacción que ha habido después.
PS: Gracias, Ignatius, por tu forma de llevar el tema. Así debería ser siempre.
Sólo le pido a Celestia que la gente que pueda considerarse mi amiga no pierda el contacto conmigo.
--·· · -·-· --- ·-· ·- ·· ··· -··· · ··· - ·--· --- -· -·--
A ver que me pierdo, referee, eres Carretonrider?
--·· · -·-· --- ·-· ·- ·· ··· -··· · ··· - ·--· --- -· -·--
A ver que me pierdo, referee, eres Carretonrider?
-

referee - Griffon

- Mensajes: 1807
- Registrado: 14 Abr 2013, 18:58
- Sexo: Masculino
- Pony preferido: Twilight Sparkle
Re: [05x09] Slice of Life
Ignatius escribió en 14 Jun 2015, 03:34:Capítulos de ese calibre ha habido y habrá. Este capítulo resulta más llamativo de lo normal debido a que rompe los esquemas habituales. Me ha encantado. Pero espero que semejantes rarezas no se repitan. Primero: porque le arrebatarían la magia a este episodio tan especial, y segundo: porque si lo especial se repite demasiado, la seria cambiaría lo que es... MLP está bien como está, y este episodio me ha parecido fantástico. Aunque no le pondría un 10 por ese HYPE super gordo que tiene. El exceso de hype suele llevar a extremos, tanto negativos, como positivos (en las opiniones).
Esto no lo digo por nadie en especial, si no en general, así que espero que no se me malinterprete. De mi opinión al respecto de la de referee ya he hablado tranquilamte con él. Y la respeto al 100% aunque no la comparta. Lo digo por si alguien comenta o piensa que me refiero concretamente a él o algo... No es el caso. Que quede bien clarito.
Si fuera de otra forma, no dudaría en dejarlo claro también.
He de decir que no puedo estar mas de acuerdo contigo, el episodio ha estado bastante bien y muy llamativo dado al cambio de esquema como ya mencionas, aun así las cosas hay que tomárselas con calma y no abusar demasiado de este tipo de guiños. Sinceramente opino que el capitulo no debería de haberse limitado únicamente a 20 minutos de duración (y así ya hacían la gracia completa), ya que se puede notar un pelin forzado con tanto contenido metido en tan poco tiempo, pero bueno ellos son los creadores ellos deciden.
 Solo queda ver como continuara la serie y cuando nos volverán a sorprender con este guiño a los fans.
Solo queda ver como continuara la serie y cuando nos volverán a sorprender con este guiño a los fans.
-

BlaueDivision - Foal

- Mensajes: 39
- Registrado: 07 Jul 2014, 01:36
- Ubicación: Granada
- Sexo: Masculino
- Pony preferido: Lyra,Luna,Queen Chr
Re: [05x09] Slice of Life
referee escribió en 14 Jun 2015, 04:37:Foxer, voy a citar parte de tu mensaje para que veas la contradicción que contiene.foxer7 escribió en 14 Jun 2015, 03:21:me refiero a k de fan service y cosas "no canon" iba la cosa. de verdad te crees k van a sacar lo de bom bom o lo de gumy otra vez??
como dice, este capitulo podria considerarse aparte, pero creo k cumple esplendidamente su funcion de soltar locuras y pasarte el capitulo diciendo "o dios!" "wtf!" "es canon!".
Y ese es el problema. Es canon. Es maldito canon y el canon es rey. Y cuando alguien te venga con el cuento de Bon Bon Agente Secreto, ve tú y dile que no es canon. Porque lo es.
Puedes decir que los comics son canon o no, puedes decir que Equestria Girls es canon o no. Pero esto? Este es el maldito episodio 9 de la quinta temporada. Y como tal, es canon.
Esto mismo, hecho por un fan, me hubiera parecido genial. Esto mismo, hecho fuera de la serie estándar como tal, me hubiera parecido genial. Pero todas esas cosas absurdas, ahora son canon. Porque este es un episodio regular, por muy número 100 que sea, de My Little Pony: Friendship is Magic, y como tal lo he valorado.
Os recuerdo a todos que hay gente que evita los spoilers de todo tipo, también. Si un episodio es terrible como episodio 83, por decir algo, también es terrible como episodio 100. Quieres hacer un especial? Hazlo, pero como extra. Así podrás afirmar que no has roto el canon. No se ha hecho así, y así lo he valorado.
Creo que cuando Foxer ha dicho "cosas no canon" se refería a "cosas que no habían sido canonizadas".
Por otra parte, a ver, han hecho "canon" cosas sobre ponis de fondo. ¡Ponis de fondo! ¿De verdad eso importa tanto para lo que es la serie en sí? ¡Si precisamente se han permitido esas cosas porque no son personajes relevantes para la serie! Además, seguramente no volvamos a ver jamás más detalles al respecto. Como mucho veremos las parejas juntas de fondo y ya.
¿De verdad, DE VERDAD no te gusta nada de lo que han hecho con ellos o en realidad te sabe mal que hayan tratado de hacer un capítulo hecho exclusivamente para contentar los fans?
-

Violent_Crimson - Griffon

- Mensajes: 2061
- Registrado: 10 Ago 2012, 13:23
- Ubicación: Xàtiva
- Sexo: Masculino
- Pony preferido: Pinkie Pie
-

Lightning - Heart of Fire

- Mensajes: 430
- Registrado: 16 Oct 2014, 14:23
- Sexo: Masculino
- Pony preferido: ayy yokse tio
Re: [05x09] Slice of Life
Episodio visto.
Cosas que me gustaron:
-El episodio, aunque esté algo enfocado a las Mane 6, funciona teniendo como protagonistas a personajes de fondo.
-Aparecen muchos de los personajes de fondo de la serie: Derpy, Doctor Whooves, Octavia, Vinyl Scratch, Bon bon, Lyra... hasta Button, que tuvo su momento cumbre en, irónicamente, algo hecho por un fan y que lo vetó Hasbro. ¡Hasta sale Steven Magnet, la serpiente de mar de la primera temporada!
-La palabra "Man", sobretodo cuando lo expresa el Doctor. Hay algo en ella que me hace gracia. Quizás sea el contexto.
-La carrera que se pegan Octavia y Vinyl de camino a la boda. Muy épico, probablemente la mejor escena del episodio. Y ese monólogo es la leche.
Cosas que no me gustaron:
-La repetición de la broma The horror, the horror". Aparentemente no quieren evitar reciclar y repetir momentos geniales de la primera temporada hasta hacerlos tan carentes de humor como una sitcom barata.
-Los "lens flare" de la música de Octavia y Vinyl. No sé, me hubiera gustado ver algo más claro o más simpático. Pero tirar de lucecitas...
-El episodio habría estado mejor si pusieran al abejorro-oso destrozando Ponyville sin las Mane 6 y con Bon bon. Daría lugar a una escena bastante épica.
-El final es cursi no, lo siguiente.
-¿No habría sido mejor llamarla Derpy en lugar de Muffins? Creo que desde hace un año que la gente no es tiquismiquis con detalles como esos.
No sé. Al igual que Princess Twilight Sparkle y Twilight's Kingdom, éste debería ser mi episodio favorito. A ver, me gustó. ¿Es épico? A ratos. ¿Es gracioso? A ratos. ¿Un 10? Nah, no creo. Sólo merece la pena por ver a personajes de fondo que nos gustan y la carrera a contrarreloj. Al menos es de los mejores episodios de la temporada, aunque eso era la mar de fácil. Hay quien dice que este episodio rompe con lo habitual de la serie. Si no hubieran aparecido las Mane 6, les daría la razón.
Cosas que me gustaron:
-El episodio, aunque esté algo enfocado a las Mane 6, funciona teniendo como protagonistas a personajes de fondo.
-Aparecen muchos de los personajes de fondo de la serie: Derpy, Doctor Whooves, Octavia, Vinyl Scratch, Bon bon, Lyra... hasta Button, que tuvo su momento cumbre en, irónicamente, algo hecho por un fan y que lo vetó Hasbro. ¡Hasta sale Steven Magnet, la serpiente de mar de la primera temporada!
-La palabra "Man", sobretodo cuando lo expresa el Doctor. Hay algo en ella que me hace gracia. Quizás sea el contexto.
-La carrera que se pegan Octavia y Vinyl de camino a la boda. Muy épico, probablemente la mejor escena del episodio. Y ese monólogo es la leche.
Cosas que no me gustaron:
-La repetición de la broma The horror, the horror". Aparentemente no quieren evitar reciclar y repetir momentos geniales de la primera temporada hasta hacerlos tan carentes de humor como una sitcom barata.
-Los "lens flare" de la música de Octavia y Vinyl. No sé, me hubiera gustado ver algo más claro o más simpático. Pero tirar de lucecitas...
-El episodio habría estado mejor si pusieran al abejorro-oso destrozando Ponyville sin las Mane 6 y con Bon bon. Daría lugar a una escena bastante épica.
-El final es cursi no, lo siguiente.
-¿No habría sido mejor llamarla Derpy en lugar de Muffins? Creo que desde hace un año que la gente no es tiquismiquis con detalles como esos.
No sé. Al igual que Princess Twilight Sparkle y Twilight's Kingdom, éste debería ser mi episodio favorito. A ver, me gustó. ¿Es épico? A ratos. ¿Es gracioso? A ratos. ¿Un 10? Nah, no creo. Sólo merece la pena por ver a personajes de fondo que nos gustan y la carrera a contrarreloj. Al menos es de los mejores episodios de la temporada, aunque eso era la mar de fácil. Hay quien dice que este episodio rompe con lo habitual de la serie. Si no hubieran aparecido las Mane 6, les daría la razón.
Última edición por Ring Team el 14 Jun 2015, 11:06, editado 1 vez en total

-

Ring Team - Expulsado/a

- Mensajes: 1233
- Registrado: 16 Sep 2012, 15:47
- Pony preferido: Apple Bloom
Re: [05x09] Slice of Life
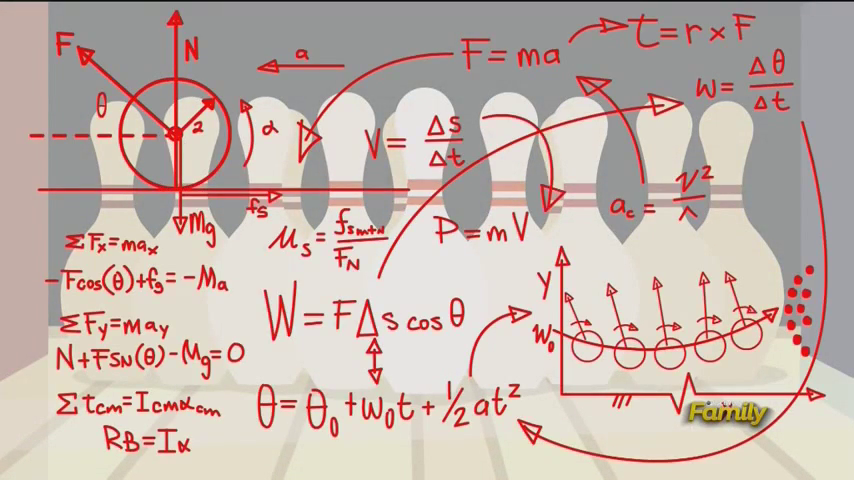
No todas son correctas, por ejemplo, en el esquema de fuerzas, si tomamos fs como la velocidad (por ponerle algo, porque no corresponde a nada), la flecha de a como la aceleración (correcta), no existe rozamiento ya que la fuerza aplicada en contra del movimiento está en ángulo con la horizontal. Si es la fuerza que aplica el Dr., también estaría mal, puesto que es a favor del movimiento, y si es cuando se encuentra en mitad del carril, también estaría mal, ya que solo está presente en ese caso la de rozamiento, que es paralela al plano donde se aplica y en la base del cuerpo.
El sumatorio de las fuerzas en X empieza bien según ese esquema de fuerzas, pero no sé de dónde sale fg.
Parece que luego intenta hallar el coeficiente de rozamiento, a través de la fuerza de rozamiento y la Normal, otra vez mal, puesto que si Fr=N*μ, μ=Fr/N, está al revés, sin contar que no se utilizaría la normal en su totalidad, puesto que existe (todo esto según su esquema de fuerzas), una fuerza que contrarresta a la del peso del cuerpo, haciendo que la Normal valga menos.
Él cálculo del trabajo está bien, todo se tiene que decir, pero llama a Δs, θ, que se supone que ya es el ángulo, aparte θ sub 0 sobra, ya que la posición inicial con respecto al lanzador es 0 (discutible ya que se puede escoger otro sistema de referencia). De ahí sale que la potencia es la variación de trabajo con respecto a la de tiempo, correcta.
La fórmula que más tendría que haber desarrollado sería la de del movimiento lineal (P=mV), pero se queda ahí, solo indicando que la velocidad es la variación de espacio con respecto al tiempo, también correcta.
Arriba, en la segunda ley de Newton, los cálculos son correctos, la aceleración en un MCUA es la velocidad al cuadrado partido el radio de giro (suponiendo que ese "circunflejo" sea r, lo daremos por válido)
Si unimos todos los cálculos en la gráfica (creo que los puntos son los bolos) nos daremos cuenta de resultados imcompatibles. la fórmula usada en la variación del espacio es para la de un MRUA, no completamente válida ya que se trata de un movimiento curvilíneo. Si suponemos que la flecha grande en la bola es la fuerza centrípeta (calculada anteriormente, Fc=m*an), también está mal representada, porque si se trata de un movimiento uniformemente acelerado, siempre es igual, pero siempre cambia, pero si no se tratase de ese tipo de movimiento, también estaría mal, puesto que siempre es perpendicular al vector movimiento, por lo que el trabajo que se suponía que había calculado es 0, ya que la fuerza por el coseno de 90 es igual a 0.
Por último, t=r*F no me ha quedado muy claro, y ese 2 en el radio de la bola es un misterio.
-

Lightning - Heart of Fire

- Mensajes: 430
- Registrado: 16 Oct 2014, 14:23
- Sexo: Masculino
- Pony preferido: ayy yokse tio
Re: [05x09] Slice of Life
referee escribió en 14 Jun 2015, 04:37:Foxer, voy a citar parte de tu mensaje para que veas la contradicción que contiene.foxer7 escribió en 14 Jun 2015, 03:21:me refiero a k de fan service y cosas "no canon" iba la cosa. de verdad te crees k van a sacar lo de bom bom o lo de gumy otra vez??
como dice, este capitulo podria considerarse aparte, pero creo k cumple esplendidamente su funcion de soltar locuras y pasarte el capitulo diciendo "o dios!" "wtf!" "es canon!".
Y ese es el problema. Es canon. Es maldito canon y el canon es rey. Y cuando alguien te venga con el cuento de Bon Bon Agente Secreto, ve tú y dile que no es canon. Porque lo es.
Puedes decir que los comics son canon o no, puedes decir que Equestria Girls es canon o no. Pero esto? Este es el maldito episodio 9 de la quinta temporada. Y como tal, es canon.
Esto mismo, hecho por un fan, me hubiera parecido genial. Esto mismo, hecho fuera de la serie estándar como tal, me hubiera parecido genial. Pero todas esas cosas absurdas, ahora son canon. Porque este es un episodio regular, por muy número 100 que sea, de My Little Pony: Friendship is Magic, y como tal lo he valorado.
Os recuerdo a todos que hay gente que evita los spoilers de todo tipo, también. Si un episodio es terrible como episodio 83, por decir algo, también es terrible como episodio 100. Quieres hacer un especial? Hazlo, pero como extra. Así podrás afirmar que no has roto el canon. No se ha hecho así, y así lo he valorado.
Un usuario de este foro me ha pedido que explicara los motivos de mi nota, y lo he hecho. No me hagáis decir que pienso de la reacción que ha habido después.
PS: Gracias, Ignatius, por tu forma de llevar el tema. Así debería ser siempre.
Referee, estas sacando las cosas de quicio. A mi tampoco me ha gustado el capitulo tanto como a la gente de por aqui, pero no me he puesto a tener una pataleta y darle un 0 por una estupidez. Que han hecho un epico capitulo para el fandom pero un mal capitulo de MLP, de acuerdo, pero no es para intentar "defender" cosas indefendibles, como es lo que has hecho tu. A parte, que pasa has visto un capitulo con el sonido desincronizado, animacion hecha por parvulario y voces que parecen un grupo de sapos siendo pisados y niños llorando? porque si no es asi vuelvo a insistir que esta valoración no es normal
-

zelgadis - Background Pony

- Mensajes: 1208
- Registrado: 04 Dic 2012, 19:37
- Sexo: Masculino
- Pony preferido: twilight sparkle
Re: [05x09] Slice of Life
Referee, ¿qué te ha pasado? xD Sabemos de Larson toca muy a menudo las narices, pero hizo un episodio decente.

-

Ring Team - Expulsado/a

- Mensajes: 1233
- Registrado: 16 Sep 2012, 15:47
- Pony preferido: Apple Bloom
Re: [05x09] Slice of Life
Ha sido un capítulo bastante divertido y diferente, una sucesión de cosas muy random y que para nada es un slice of life XD
El capítulo es muy fresco comparados con los otros que tiene la serie, pero para nada me parece un capítulo de 10, porque no me ha gustado como otros capítulos. Tiene sus cosas buenas como la aparición de Doctor Whooves, los de El Gran Lebowski, la vuelta en escena de Steven Magnet o el momento de Gummy, luego tiene otras cosas que me han dejado muy frío como lo de Bon Bon y Lyra o la parte de las tías de las flores.
Para mí, un fallo muy grande es que Doctor Whooves debería de haber tenido un acento mucho más británico, han captado su esencia con esos primeros planos a su cara, sus momentos de "eureka" o esas dudas que tiene siempre hablando para si mismo. Derpy, un personaje que me parece muy sobrevalorado por el fandom me ha gustado mucho en este capítulo e incluso la parte de Octavia y Vinyl me gustó, aunque menos, me pareció demasiado marcado por el fandom. Ah, y que los otros dos personajes de "El Gran Lebowski", Walter y Donny, deberían haber tenido alguna frase, sobre todo Donny que me encanta la voz que tiene Steve Buscemi.
Lo dicho, un buen capítulo de humor, que será recordado para siempre entre los fans de la serie por ser el primer contacto con el fandom, y espero que sea el último. Que este sea el primer y único capítulo dedicado al fandom, por favor. Una serie puede tener en cuenta a los fans pero nunca sobrepasar esa línea de depender de ellos para hacer un capítulo que harían los propios fans, si la serie ha llegado tan lejos y tiene tantos fans y sin ningún capítulo totalmente para el fandom, ¿por qué empezar ahora?
-Lo dicho un capítulo de 7-8 para mí, divertida pero no perfecta. Y como dije antes: "Todo por el fandom, pero sin el fandom"
El capítulo es muy fresco comparados con los otros que tiene la serie, pero para nada me parece un capítulo de 10, porque no me ha gustado como otros capítulos. Tiene sus cosas buenas como la aparición de Doctor Whooves, los de El Gran Lebowski, la vuelta en escena de Steven Magnet o el momento de Gummy, luego tiene otras cosas que me han dejado muy frío como lo de Bon Bon y Lyra o la parte de las tías de las flores.
Para mí, un fallo muy grande es que Doctor Whooves debería de haber tenido un acento mucho más británico, han captado su esencia con esos primeros planos a su cara, sus momentos de "eureka" o esas dudas que tiene siempre hablando para si mismo. Derpy, un personaje que me parece muy sobrevalorado por el fandom me ha gustado mucho en este capítulo e incluso la parte de Octavia y Vinyl me gustó, aunque menos, me pareció demasiado marcado por el fandom. Ah, y que los otros dos personajes de "El Gran Lebowski", Walter y Donny, deberían haber tenido alguna frase, sobre todo Donny que me encanta la voz que tiene Steve Buscemi.
Lo dicho, un buen capítulo de humor, que será recordado para siempre entre los fans de la serie por ser el primer contacto con el fandom, y espero que sea el último. Que este sea el primer y único capítulo dedicado al fandom, por favor. Una serie puede tener en cuenta a los fans pero nunca sobrepasar esa línea de depender de ellos para hacer un capítulo que harían los propios fans, si la serie ha llegado tan lejos y tiene tantos fans y sin ningún capítulo totalmente para el fandom, ¿por qué empezar ahora?
-Lo dicho un capítulo de 7-8 para mí, divertida pero no perfecta. Y como dije antes: "Todo por el fandom, pero sin el fandom"
Última edición por stefanopl2 el 14 Jun 2015, 11:36, editado 1 vez en total
Resultado Test de Personalidad de Ponies --> http://oi42.tinypic.com/21oao8w.jpg

TWITTER: http://twitter.com/stefanopl2
CANAL DE BLACKITALIAN: http://www.youtube.com/user/lBlackitalian/videos

TWITTER: http://twitter.com/stefanopl2
CANAL DE BLACKITALIAN: http://www.youtube.com/user/lBlackitalian/videos
-

stefanopl2 - CMC

- Mensajes: 399
- Registrado: 28 Nov 2013, 16:00
- Ubicación: Rincón de la Victoria (Málaga)
- Sexo: Masculino
- Pony preferido: Applejack, RD, Luna
-

Duster_Seamus - Moon Rock

- Mensajes: 2603
- Registrado: 08 Sep 2013, 22:22
- Ubicación: A veces en casa, a veces no
- Sexo: Masculino
- Pony preferido: RD/Derpy/Discord
Re: [05x09] Slice of Life
stefanopl2 escribió en 14 Jun 2015, 11:23: Ah, y que los otros dos personajes de "El Gran Lebowski", Walter y Donny, deberían haber tenido alguna frase, sobre todo Donny que me encanta la voz que tiene Steve Buscemi.
Para que ponerle voz a Donny si cuando abriese la boca le iban a gritar que se callase?

Y por cierto, el Changeling viene a confirmar una de las frases que se digeron en la SDCC sobre si Chrysalis haría acto de presencia esta temporada. La respuesta en su dia fue "en espíritu al menos". Que salga un changeling ahora significa que al menos no se han olvidado de ellos

-

McDohl - Guardia de Canterlot

- Mensajes: 7422
- Registrado: 23 Sep 2012, 20:50
- Ubicación: Feeling like Macdolia...
- Sexo: Masculino
- Pony preferido: Derpy Hooves
Re: [05x09] Slice of Life
Creo qué este se ha convertido en uno de mis capítulos favoritos xD
Estoy muy contento, querían ofrecer un capítulo dedicado al fandom y en mi opinión lo han logrado. Me lo he bajado porque estoy hay tenerlo guardado durante un buen tiempo.
-¡Derpy mi yeguita vuelve a hablar! Y no se ha contenido. ¡TE QUIERO! Aunque en parte entiendo que la hayan querido llamar "Muffins", imagino que Hasbro no quería arriesgarse en hacerla relacionar con enfermedades mentales, los "Flanders" pueden saltar a la mínima.
-Filosofogummy, nuevo meme.
-Allons-Y! Aunque al final Tennant no le haya dado voz han sabido darle muy bien la actitud del Doctor a Doctor Hooves, me ha gustado el "guiño" de la bufanda del final.
-Shipping, ahora Lyrabon, Octanyl y Derpydoctor son canon xD
-La foto de las máscaras, wtf?
-El discurso de la alcaldesa durante la boda me ha tocado la fibra: No solos los protagonistas tienen un papel, todos tienen una historia.
-La mudez de Vinyl se hace canon, aunque para algunos siempre estará Nowacking. Yo la prefiero muda.
-El Changeling me ha matado xD el pobre sólo quería su porción de amor.
¿Nota? A riesgo de sonar fanboy he puesto Hype xD es que no siento nada más ahora mismo.
Estoy muy contento, querían ofrecer un capítulo dedicado al fandom y en mi opinión lo han logrado. Me lo he bajado porque estoy hay tenerlo guardado durante un buen tiempo.
-¡Derpy mi yeguita vuelve a hablar! Y no se ha contenido. ¡TE QUIERO! Aunque en parte entiendo que la hayan querido llamar "Muffins", imagino que Hasbro no quería arriesgarse en hacerla relacionar con enfermedades mentales, los "Flanders" pueden saltar a la mínima.
-Filosofogummy, nuevo meme.
-Allons-Y! Aunque al final Tennant no le haya dado voz han sabido darle muy bien la actitud del Doctor a Doctor Hooves, me ha gustado el "guiño" de la bufanda del final.
-Shipping, ahora Lyrabon, Octanyl y Derpydoctor son canon xD
-La foto de las máscaras, wtf?
-El discurso de la alcaldesa durante la boda me ha tocado la fibra: No solos los protagonistas tienen un papel, todos tienen una historia.
-La mudez de Vinyl se hace canon, aunque para algunos siempre estará Nowacking. Yo la prefiero muda.
-El Changeling me ha matado xD el pobre sólo quería su porción de amor.
¿Nota? A riesgo de sonar fanboy he puesto Hype xD es que no siento nada más ahora mismo.
-

Akakun - Background Pony

- Mensajes: 1351
- Registrado: 03 Mar 2014, 01:33
- Ubicación: Córdoba
- Sexo: Masculino
- Pony preferido: Derpy, Discord, SS
Re: [05x09] Slice of Life
McDohl escribió en 14 Jun 2015, 11:50:stefanopl2 escribió en 14 Jun 2015, 11:23: Ah, y que los otros dos personajes de "El Gran Lebowski", Walter y Donny, deberían haber tenido alguna frase, sobre todo Donny que me encanta la voz que tiene Steve Buscemi.
Para que ponerle voz a Donny si cuando abriese la boca le iban a gritar que se callase?
Y por cierto, el Changeling viene a confirmar una de las frases que se digeron en la SDCC sobre si Chrysalis haría acto de presencia esta temporada. La respuesta en su dia fue "en espíritu al menos". Que salga un changeling ahora significa que al menos no se han olvidado de ellos
Vale, ahora tengo mucho miedo. De ahí puede salir algo muuuy bueno o algo muuuy malo. O, siendo generosos, algo demasiado normal para rescatar un personaje como ese.

-

Ring Team - Expulsado/a

- Mensajes: 1233
- Registrado: 16 Sep 2012, 15:47
- Pony preferido: Apple Bloom
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 0 invitados